Asymptotics and Fourier Expansions of the Sequence of Linear Factor of Polynomials Orthogonal with Gegenbauer-Sobolev Inner Product

Authors

  • Abdalgadir Albushra Sudan University of Science and Technology, Faculty of Education, Department of Mathematics, Sudan
  • Musa Siddig University of Kordofan, Faculty of Science, Department of Mathematics, Sudan
  • Amani Elseid Department of Mathematics, College of Aldayer, Jazan University, Saudi Arabia
  • Abdelrehaman Mohamsd University of Kordofan, Faculty of Science, Department of Mathematics, Sudan

DOI:

https://doi.org/10.63002/asrp.306.1110

Keywords:

Gegenbauer–Sobolev type orthogonal polynomials, Gegenbauer orthogonal polynomials, Mehler-Heine type formula, Chebyshev polynomial, Fourier expansions, higher exponents, monic Gegenbauer orthogonal polynomial, Banach-Steinhaus theorem

Abstract

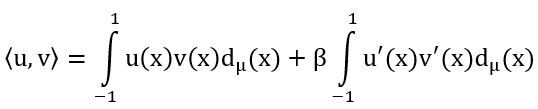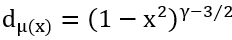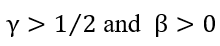For monic polynomials orthogonal to the non-discrete Sobolev inner product, let mceclip0.pngshow the sequence of quadratic factors. mceclip1.png. Where mceclip2.png with mceclip3.png . Both Sobolev norms of 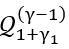mceclip4.pngand a Mehler-Heine type formula with a strong asymptotic on  are obtained. Additionally, we look for the necessary conditions for norm convergence and the reasons for the norm convergence of a Fourier expansion, specifically with regard to the Sobolev orthogonal polynomials.

Downloads

Published

06-11-2025

Issue

Vol. 3 No. 06 (2025): Applied Sciences Research Periodicals

Section

Articles

License

Copyright (c) 2025 Abdalgadir Albushra, Musa Siddig, Amani Elseid, Abdelrehaman Mohamsd

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.